algorithms.statistics.models.model

Module: algorithms.statistics.models.model

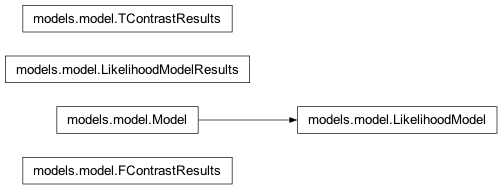
Inheritance diagram for nipy.algorithms.statistics.models.model:

Classes

FContrastResults

class nipy.algorithms.statistics.models.model.FContrastResults(effect, covariance, F, df_num, df_den=None)

Bases: object

Results from an F contrast of coefficients in a parametric model.

The class does nothing, it is a container for the results from F contrasts, and returns the F-statistics when np.asarray is called.

__init__(effect, covariance, F, df_num, df_den=None)

LikelihoodModel

class nipy.algorithms.statistics.models.model.LikelihoodModel

Bases: Model

__init__()

fit()

Fit a model to data.

information(theta, nuisance=None)

Fisher information matrix

The inverse of the expected value of - d^2 logL / dtheta^2.

initialize()

Initialize (possibly re-initialize) a Model instance.

For instance, the design matrix of a linear model may change and some things must be recomputed.

logL(theta, Y, nuisance=None)

Log-likelihood of model.

predict(design=None)

After a model has been fit, results are (assumed to be) stored in self.results, which itself should have a predict method.

score(theta, Y, nuisance=None)

Gradient of logL with respect to theta.

This is the score function of the model

LikelihoodModelResults

class nipy.algorithms.statistics.models.model.LikelihoodModelResults(theta, Y, model, cov=None, dispersion=1.0, nuisance=None, rank=None)

Bases: object

Class to contain results from likelihood models

__init__(theta, Y, model, cov=None, dispersion=1.0, nuisance=None, rank=None)

Set up results structure

Parameters:

thetandarray

parameter estimates from estimated model

Yndarray

data

modelLikelihoodModel instance

model used to generate fit

covNone or ndarray, optional

covariance of thetas

dispersionscalar, optional

multiplicative factor in front of cov

nuisanceNone of ndarray

parameter estimates needed to compute logL

rankNone or scalar

rank of the model. If rank is not None, it is used for df_model instead of the usual counting of parameters.

Notes

The covariance of thetas is given by:

dispersion * cov

For (some subset of models) dispersion will typically be the mean square error from the estimated model (sigma^2)

AIC()

Akaike Information Criterion

BIC()

Schwarz’s Bayesian Information Criterion

Fcontrast(matrix, dispersion=None, invcov=None)

Compute an Fcontrast for a contrast matrix matrix.

Here, matrix M is assumed to be non-singular. More precisely

\[M pX pX' M'\]

is assumed invertible. Here, \(pX\) is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full.

See the contrast module to see how to specify contrasts. In particular, the matrices from these contrasts will always be non-singular in the sense above.

Parameters:

matrix1D array-like

contrast matrix

dispersionNone or float, optional

If None, use self.dispersion

invcovNone or array, optional

Known inverse of variance covariance matrix. If None, calculate this matrix.

Returns:

f_resFContrastResults instance

with attributes F, df_den, df_num

Notes

For F contrasts, we now specify an effect and covariance

Tcontrast(matrix, store=('t', 'effect', 'sd'), dispersion=None)

Compute a Tcontrast for a row vector matrix

To get the t-statistic for a single column, use the ‘t’ method.

Parameters:

matrix1D array-like

contrast matrix

storesequence, optional

components of t to store in results output object. Defaults to all components (‘t’, ‘effect’, ‘sd’).

dispersionNone or float, optional

Returns:

resTContrastResults object

conf_int(alpha=0.05, cols=None, dispersion=None)

The confidence interval of the specified theta estimates.

Parameters:

alphafloat, optional

The alpha level for the confidence interval. ie., alpha = .05 returns a 95% confidence interval.

colstuple, optional

cols specifies which confidence intervals to return

dispersionNone or scalar

scale factor for the variance / covariance (see class docstring and vcov method docstring)

Returns:

cisndarray

cis is shape (len(cols), 2) where each row contains [lower, upper] for the given entry in cols

Notes

Confidence intervals are two-tailed. TODO: tails : string, optional

tails can be “two”, “upper”, or “lower”

Examples

>>> from numpy.random import standard_normal as stan
>>> from nipy.algorithms.statistics.models.regression import OLSModel
>>> x = np.hstack((stan((30,1)),stan((30,1)),stan((30,1))))
>>> beta=np.array([3.25, 1.5, 7.0])
>>> y = np.dot(x,beta) + stan((30))
>>> model = OLSModel(x).fit(y)
>>> confidence_intervals = model.conf_int(cols=(1,2))

logL()

The maximized log-likelihood

t(column=None)

Return the (Wald) t-statistic for a given parameter estimate.

Use Tcontrast for more complicated (Wald) t-statistics.

vcov(matrix=None, column=None, dispersion=None, other=None)

Variance/covariance matrix of linear contrast

Parameters:

matrix: (dim, self.theta.shape[0]) array, optional

numerical contrast specification, where dim refers to the ‘dimension’ of the contrast i.e. 1 for t contrasts, 1 or more for F contrasts.

column: int, optional

alternative way of specifying contrasts (column index)

dispersion: float or (n_voxels,) array, optional

value(s) for the dispersion parameters

other: (dim, self.theta.shape[0]) array, optional

alternative contrast specification (?)

Returns:

cov: (dim, dim) or (n_voxels, dim, dim) array

the estimated covariance matrix/matrices

Returns the variance/covariance matrix of a linear contrast of the

estimates of theta, multiplied by dispersion which will often be an

estimate of dispersion, like, sigma^2.

The covariance of interest is either specified as a (set of) column(s)

or a matrix.

Model

class nipy.algorithms.statistics.models.model.Model

Bases: object

A (predictive) statistical model.

The class Model itself does nothing but lays out the methods expected of any subclass.

__init__()

fit()

Fit a model to data.

initialize()

Initialize (possibly re-initialize) a Model instance.

For instance, the design matrix of a linear model may change and some things must be recomputed.

predict(design=None)

After a model has been fit, results are (assumed to be) stored in self.results, which itself should have a predict method.

TContrastResults

class nipy.algorithms.statistics.models.model.TContrastResults(t, sd, effect, df_den=None)

Bases: object

Results from a t contrast of coefficients in a parametric model.

The class does nothing, it is a container for the results from T contrasts, and returns the T-statistics when np.asarray is called.

__init__(t, sd, effect, df_den=None)