algorithms.statistics.models.family.links

Module: algorithms.statistics.models.family.links

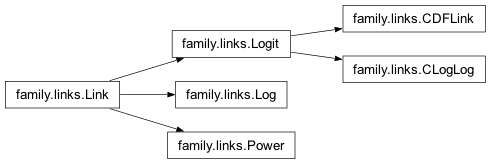
Inheritance diagram for nipy.algorithms.statistics.models.family.links:

Classes

CDFLink

class nipy.algorithms.statistics.models.family.links.CDFLink(dbn=<scipy.stats._continuous_distns.norm_gen object>)

Bases: Logit

The use the CDF of a scipy.stats distribution as a link function:

g(x) = dbn.ppf(x)

__init__(dbn=<scipy.stats._continuous_distns.norm_gen object>)

clean(p)

Clip logistic values to range (tol, 1-tol)

INPUTS:

p – probabilities

OUTPUTS: pclip

pclip – clipped probabilities

deriv(p)

Derivative of CDF link

g(p) = 1/self.dbn.pdf(self.dbn.ppf(p))

INPUTS:

x – mean parameters

OUTPUTS: z

z – derivative of CDF transform of x

initialize(Y)

inverse(z)

Derivative of CDF link

g(z) = self.dbn.cdf(z)

INPUTS:

z – linear predictors in GLM

OUTPUTS: p

p – inverse of CDF link of z

tol = 1e-10

CLogLog

class nipy.algorithms.statistics.models.family.links.CLogLog

Bases: Logit

The complementary log-log transform as a link function:

g(x) = log(-log(x))

__init__(*args, **kwargs)

clean(p)

Clip logistic values to range (tol, 1-tol)

INPUTS:

p – probabilities

OUTPUTS: pclip

pclip – clipped probabilities

deriv(p)

Derivatve of C-Log-Log transform

g(p) = - 1 / (log(p) * p)

INPUTS:

p – mean parameters

OUTPUTS: z

z – - 1 / (log(p) * p)

initialize(Y)

inverse(z)

Inverse of C-Log-Log transform

g(z) = exp(-exp(z))

INPUTS:

z – linear predictor scale

OUTPUTS: p

p – mean parameters

tol = 1e-10

Link

class nipy.algorithms.statistics.models.family.links.Link

Bases: object

A generic link function for one-parameter exponential family, with call, inverse and deriv methods.

__init__(*args, **kwargs)

deriv(p)

initialize(Y)

inverse(z)

Log

class nipy.algorithms.statistics.models.family.links.Log

Bases: Link

The log transform as a link function:

g(x) = log(x)

__init__(*args, **kwargs)

clean(x)

deriv(x)

Derivative of log transform

g(x) = 1/x

INPUTS:

x – mean parameters

OUTPUTS: z

z – derivative of log transform of x

initialize(Y)

inverse(z)

Inverse of log transform

g(x) = exp(x)

INPUTS:

z – linear predictors in GLM

OUTPUTS: x

x – exp(z)

tol = 1e-10

Logit

class nipy.algorithms.statistics.models.family.links.Logit

Bases: Link

The logit transform as a link function:

g’(x) = 1 / (x * (1 - x)) g^(-1)(x) = exp(x)/(1 + exp(x))

__init__(*args, **kwargs)

clean(p)

Clip logistic values to range (tol, 1-tol)

INPUTS:

p – probabilities

OUTPUTS: pclip

pclip – clipped probabilities

deriv(p)

Derivative of logit transform

g(p) = 1 / (p * (1 - p))

INPUTS:

p – probabilities

OUTPUTS: y

y – derivative of logit transform of p

initialize(Y)

inverse(z)

Inverse logit transform

h(z) = exp(z)/(1+exp(z))

INPUTS:

z – logit transform of p

OUTPUTS: p

p – probabilities

tol = 1e-10

Power

class nipy.algorithms.statistics.models.family.links.Power(power=1.0)

Bases: Link

The power transform as a link function:

g(x) = x**power

__init__(power=1.0)

deriv(x)

Derivative of power transform

g(x) = self.power * x**(self.power - 1)

INPUTS:

x – mean parameters

OUTPUTS: z

z – derivative of power transform of x

initialize(Y)

inverse(z)

Inverse of power transform

g(x) = x**(1/self.power)

INPUTS:

z – linear predictors in GLM

OUTPUTS: x

x – mean parameters